Freely-Rotating Chain and Characteristic Ratio
A model that describes polymer chains in the absence of long-range self-interactions is the freely rotating chain. The bond angles of such a chain are fixed to a constant value θ, but each bond is allowed to freely rotate about the backbone in the direction of the preceding bond vector (see figure below). In others words all torsional angles φ about each bond along the backbone are equally probable. Then the conformation of a linear polymer chain can be expressed in terms of n−1 dihedral bond angles.
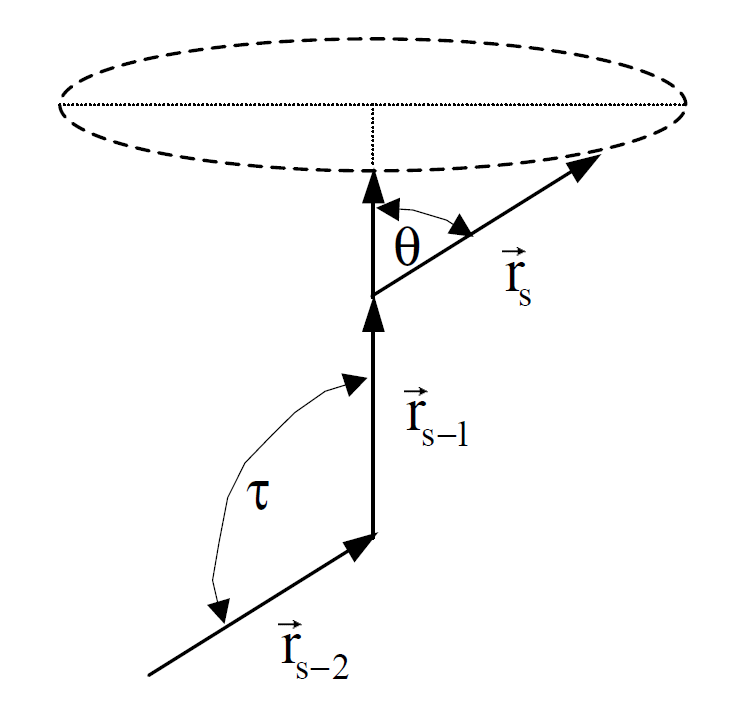
Using the vector approach, it can be shown that the projection of the sth bond on the (s-1)th bond is cos θ and the projection of this projection on the (s-2)th bond is (cos θ)2, etc.
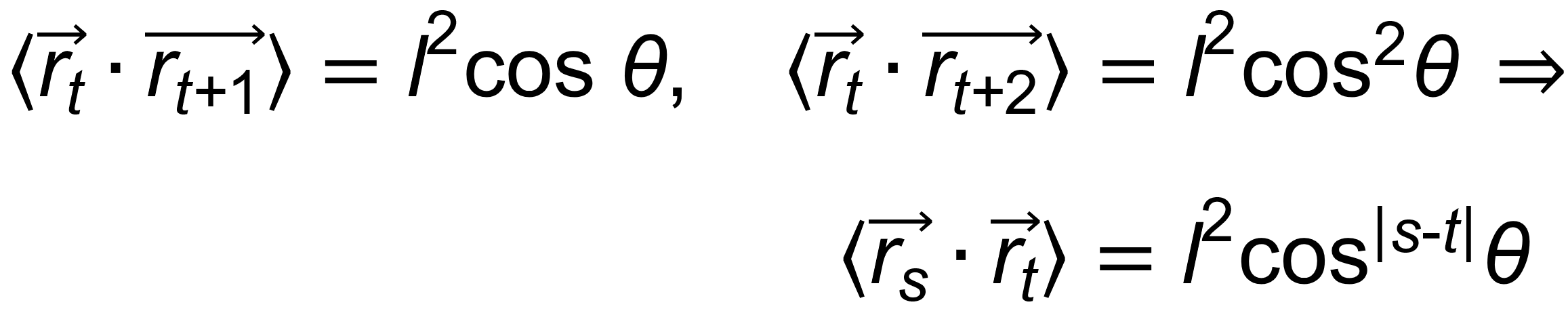
The mean square end-to-end vector of a freely rotating chain can be written as
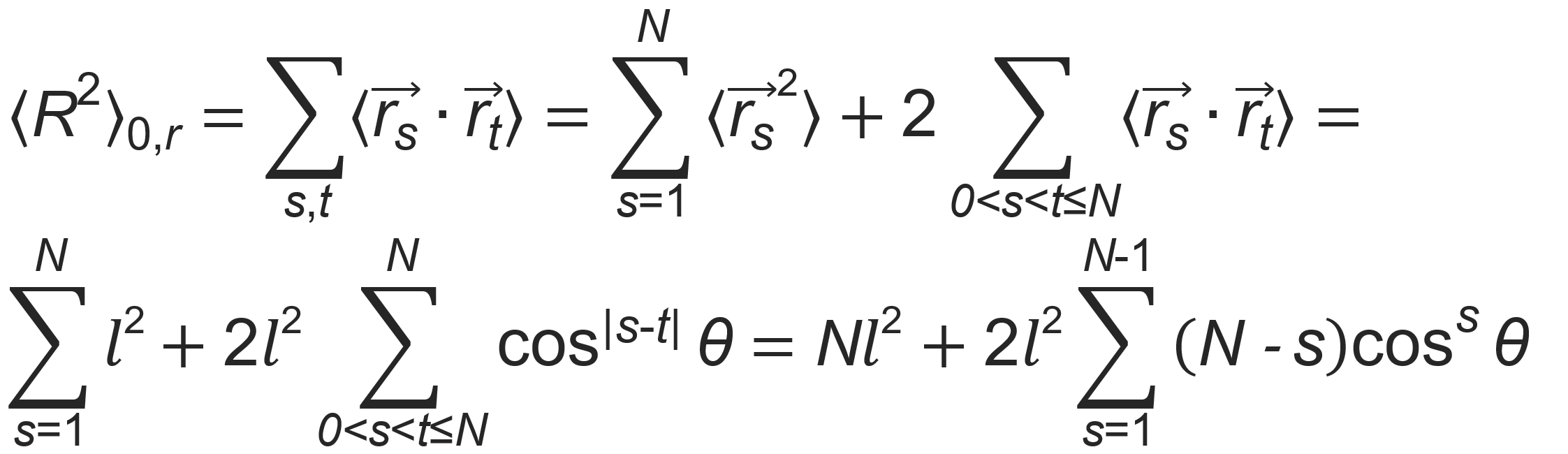
The sum is a geometric series in cos θ. With some algebraic manipulation we obtain
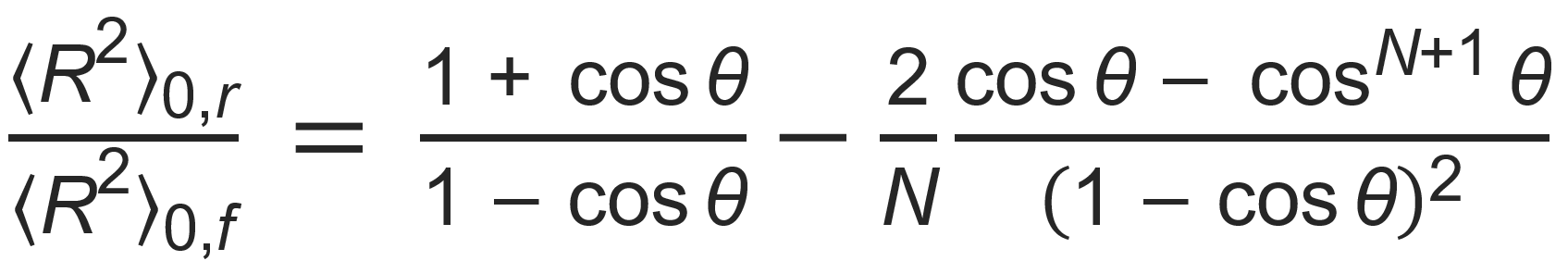
where 〈R2⟩0,f = N l 2 is the mean square end-to-end distance of a hypothetical chain with no restrictions on the bond angles and with the same number and length of bonds (Gaussian or freely-jointed chain). For infinitely long polymer chains the second term in the equation above may be neglected and the above ratio reduces to
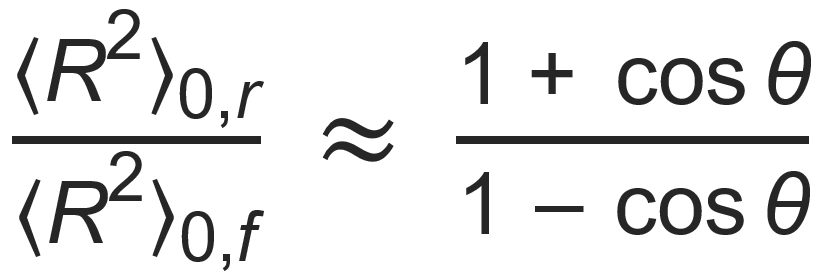
If we assume tetrahedral bond angles between consecutive bonds (τ = 109.5° ⇒ θ = 70.5°) and impose no other restrictions (no steric interaction), the mean-square distance of the chain ends, ⟨R2⟩0,r, increases by about a factor of two compared to a freely jointed chain, 〈R2⟩0,f :1,2
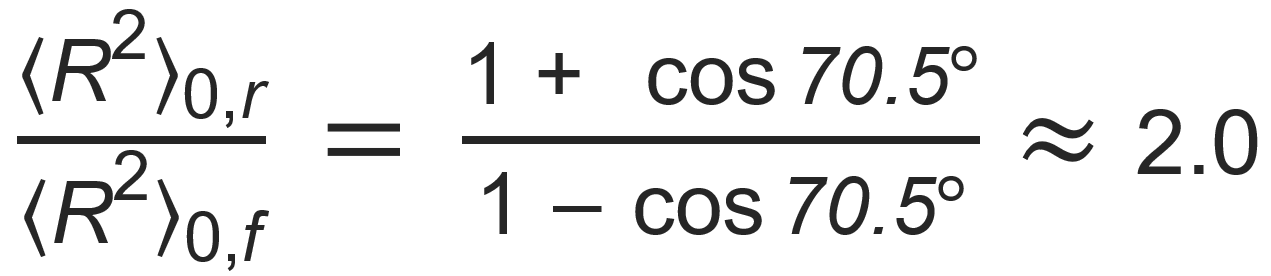
In real polymer chains the rotation about the backbone is restricted due to steric interactions between pendant groups (hindered internal rotation) and due to excluded-volume effects. Thus, the rotational states of neighboring bonds are not mutually independent. The excluded-volume effect simply means that two segments cannot occupy the same position in space. This effect increases with the number of repeat units, Nν, in the chain. Taking both effects into account, a characteristic ratio C∞(Nν → ∞) may be introduced as a measure of the expansion of the actual end-to-end distance of the real polymer chain compared to a hypothetical ideal chain with (statistical) bond length lν:
C∞ = 〈R2⟩0 / (Nν lν2)
where 〈R2⟩0 is the mean-square end-to-end distance of an unperturbed coiled polymer chain, Nν is the number of statistical skeletal units in the polymer chain, and lν is the root-mean-square length of such a unit. This length should not be confused with the Kuhn lenght. lν is the average end-to-end distance of a monomer unit, or in other words, a statistical skeletal unit and in some cases a real skeletal bond length which is an elementary rotational unit of the polymer. The Kuhn length, on the other hand, is twice the persistence length.6
For very flexible skeletal units, C∞ ≈ 2.0, a polymer behaves almost like a freely rotating chain. This, for example, is the case for polysulfone (C∞ = 2.2).
Another important ratio is the Stockmayer-Kurata ratio σ. It is measure for the stiffness of a chain, that is, for the rotational isomerism preferences.3
σ = (〈R2⟩0 /⟨R2⟩0,r)1/2
where 〈R2⟩0,r is the root-mean square ene-to-end distance of the hypothetical chain with same bond angles and bond length but with free rotation around the valence cone. σ is a measure of the effect of stetric hindrance on the average chain dimension.
| Compound | Experimental C∞ | Predicted C∞ |
| Polyethylene (PE) | 5.7 | 5.5 |
| Polycarbonate (PC) | 2.4 | 2.7 |
| Poly(vinyl chloride) (PVC) | 7.6 | 7.6 |
| Poly(methyl methacrylate) (PMMA) | 7.9 | 8.1 |
| i-Poly(methyl methacrylate) (iPMMA)a | 10.7 | 10.6 |
| Bisphenol A Polysulfone | 2.2 | 2.2 |
| Polycaprolactam (Nylon 6) | 6.2 | 6.0 |
| Polystyrene (PS) | 10.8 | 10.7 |
| Poly(ethylene terephthalate) (PET) | 4.10 | 3.56 |
References & Notes
Gert Strobl, The Physics of Polymers, 3rd Edition, Heidelberg 2007
T. Hesse, Polymere an Phasengrenzflaechen, First Edition, Bremen 2004
M. Kurata and W. H. Stockmayer, Adv. Polym. Sci. 3, 196 (1963)
S. Wu. Polymer International, Vol. 29, 3 (1992)
Paul J. Flory, Principles of Polymer Chemistry, 1st Edition 1953 Cornell University
The persistence length can be qualitatively described as the length along the chain backbone that one must travel before the next statistical unit no longer correlates with the end-to-end vector. For example, the persistence length of a freely jointed chain is one segment length and that of a rod like chain is equal to the end-to-end distance.